Ab initio simulation of diffractometer instrumental function for high-resolution X-ray diffraction
Modelling of resolution effects is important both for analysis of measured X-ray diffraction data and for planning of new experiments. Being provided a measured profile or a reciprocal-space map, one may ask himself which of the observed features (additional peaks, streaks, long tails of the distributions) are caused by the sample structure itself (unexpected additional crystalline layers, defects, etc.) and which ones represent just a manifestation of resolution effects (wavelength, monochromator and analyzer streaks, Cu Kα2 and Kβ lines, etc.). When planning an X-ray diffraction experiment, a scientist commonly faces a dilemma: either to choose a high-resolution configuration (narrow width- and height-limiting slits, a 4-bounce monochromator and a 2-bounce analyzer) and sacrifice the signal intensity, or to perform a fast measurement with a low relative level of shot noise, but quite large broadening of the observed peaks. To take a qualified decision, it is useful to evaluate the influence of the both effects (intensity reduction and peak broadening) on the performed analysis prior to the measurement. For some simple and commonly encountered situations, the answers to the outlined questions are well-known and available in textbooks. For more complex cases, numerical simulation or analytical modeling of the diffractometer resolution function is necessary. Here, elaborate mathematical methods and artificial intelligence come up on the stage.
There are a number of approaches to modeling resolution effects. The fundamental parameters approach [Cheary R. W. et al. (2004). J. Res. Natl. Inst. Stand. Technol. 109, 1-25; Zuev A. D. (2006). J. Appl. Cryst. 39, 304–314; O. Masson et al. (2003). J. Appl. Cryst., 36, 286.] is based on analytical profile shape generation from physically based models, depending on principal parameters. It is suitable for any laboratory diffractometer and provides high performance, but needs certain assumptions about geometry and diffractometer configuration and, therefore, requires manual adaptation for new systems. Ray tracing [Lambert S., Guillet F. (2008). J. Appl. Cryst. 41, 153–160; Yamada T. et al. (2001). J. Synchrotron Rad. 8, 1047–1050; Alianelli L. et al. (2003). J. Synchrotron Rad. 10, 191–192; L. Rebuffi, P. Scardi (2014). Proc. SPIE, 9209, 92090J; M. Sanchez del Rio et al. (2011). Synchrotron Rad., 18, 708-716] is a universal approach, well-suited for computer implementation. However, its main drawback is computational expensiveness, especially pronounced when a three-dimensional problem is considered (restriction of rays to the diffraction plane is not imposed). Another approach is empirical modeling of the diffractometer instrumental function by a simple fixed analytical function [Bruegemann L. et al. (1992). Acta Cryst. A48, 688-692; Van der Sluis P. (1994). J. Appl. Cryst. 27, 50-55] or as a convolution of several simple analytical functions [Gozzo, F. et al. (2006). J. Appl. Cryst. 39, 347–357; Sabine, T. M. (1987). J. Appl. Cryst. 20, 23–27.] with optimizable parameters. This option provides simple analytical expressions and high speed of calculation at a cost of limited accuracy and applicability of simple models, and the need for model calibration using a reference sample.
Atomicus team has developed a novel semi-analytical ray-tracing approach to modeling of resolution function, applicable to any combination of X-ray optics and any (coplanar and non-coplanar) measurement geometry, and suitable for a fully-automated realization. The purpose of our approach is to combine the universality of numerical methods with high performance of analytical approaches. Our approach is based on the following basis principles (see also the scheme in Figure 1).
- X-ray radiation intensity in each cross section of the beam is represented as a function of two spatial and two angular coordinates, characterizing considered spatial point and propagation direction, and the wavelength. In other words, we assign certain intensity to each ray. In contrast to traditional ray tracing, we do not generate a finite set of rays, but rather build analytical expressions suitable for description of any ray.
- Each X-ray optical element is characterized by its two actions: linear mapping of the ray coordinates before and after the element (i.e. deflection or compression of the rays) and change of the ray intensity according to the transmission function of the element, which depends on the ray position, direction and wavelength.
- For instrumental function calculation, the idealized sample accepting only a fixed transferred wave vector is considered. Further simulation for a realistic sample is performed by a convolution of the sample response function with the modelled resolution function.
- The detected signal is calculated by numerical integration of radiation intensity over the spatial area of the detector and over all possible propagation angles. Actual integration limits are provided by spatial and angular beam shape estimation for the considered diffractometer configuration.
The universality of the approach is provided by a simple unified description of all the optical elements. To introduce a new element, we just need to know how it deflects rays and changes the intensities (i.e. its coordinate transfer matrix and transmission function). No other assumptions or expert-level information are required. The elements, to which our approach has been applied and successfully tested, include height and width-limiting slits; 1, 2, and 4-bounce monochromators; Soller slits (flat and radial); beam expanders and compressors; focusing monochromators; micromasks; filters; Göbel mirrors and Montel optics; polycapillary X-ray lenses; etc.
High performance (1-40 s for typical simulations, in contrast to hours required by some numerical approaches) is achieved due to preserving analytical description of the rays up to the final detection stage. Instead of sampling the rays emitted by the source in all feasible directions, we consider only the rays that are likely to successfully reach the detector, their discrete set being produced only by the numerical integration procedure. First, the analytical treatment of the optical elements tremendously increases the efficiency of the rays sampling, because the rays, which are known to miss the detector for sure, are not even taken into consideration. Also, the developed adaptive integration approach chooses the density of the grid points in a smart non-uniform way, depending on the estimated shape of the resolution function, and provides an additional increase of the rays sampling efficiency. In other words, our approach implements smart ray tracing where artificial intelligence (based on adaptive treatment of the already calculated values and analytical projective description of the optical elements) decides, which of the rays are actually worth being considered.
Several examples of the approach application are shown in Figures 2 and 3.
The results are published in the following paper: A. Mikhalychev, A. Benediktovitch, T. Ulyanenkova, A. Ulyanenkov (2015). J. Appl. Cryst., 48, 679. (https://scripts.iucr.org/cgi-bin/paper?fv5029)
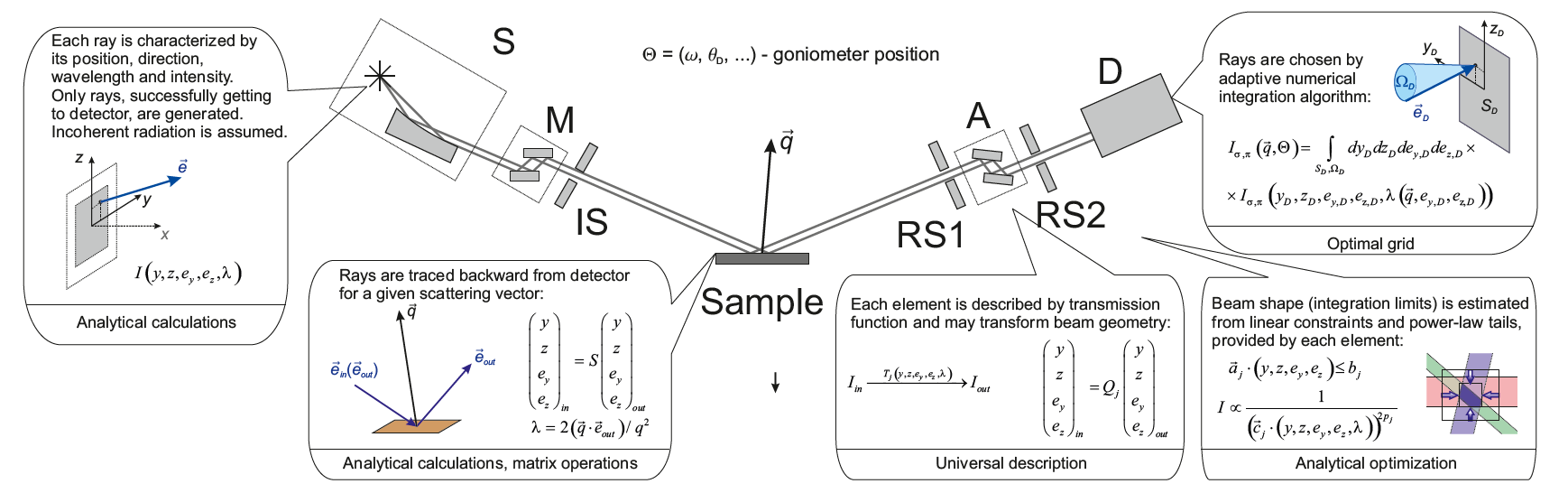
Figure 1. Schematic description of the semi-analytical ray-tracing approach.
Figure 2. An example of simulated multi-streak resolution function (0.2 mm incident slit, Ge(220)x1 analyzer, reflection 004 of silicon).
Figure 3. An example of simulated 3-dimensional shape of resolution function in the reciprocal space (1 mm incident slit, Ge(220)x2 monochomator, 2 x 0.2 mm receiving slits, Ge(220)x2 analyzer, reflection 004 of silicon).


