Artificial intelligence: Bayesian approach to automatic peak indexing in HRXRD
Position and width of peaks in high-resolution X-ray diffraction (HRXRD) data (profiles and reciprocal space maps) carry the information, which can be used for computationally effective analysis of the sample structure [V. Holý et al, Adv. Nat. Sci: Nanosci. Nanotechnol., 2017, 8 015006; A. Benediktovitch et al., Theoretical Concepts of X-Ray Nanoscale Analysis: Theory and Applications (Springer, 2014); Chu Ryang Wie, Materials Science and Engineering: R: Reports, 1994, 13:1–56; B. K. Tanner, Journal of Crystal Growth, 1990, 99: 1315-1323]. Before estimation of the sample parameters, one needs to index the peaks, present in the measured data, by finding the correct correspondence between each measured peak with an expected Bragg peak, a layer thickness oscillation fringe or a superlattice fringe. Artificial intelligence-based automatic peak indexing is a step towards fully automated data processing and can provide reproducible results, free of human errors. To design a peak indexing algorithm, one can either “guess” the procedure, which mimics the manual peak indexing, or derive the algorithm from physically grounded principles. The latter approach is preferable since it can be made universal, free of ad hoc assumptions, suitable for further modifications, and much clearer from the theoretical point of view. Atomicus team implemented that option on the basis of Bayesian approach, previously shown to be effective for analysis of powder X-ray diffraction data [A. Mikhalychev, A. Ulyanenkov, J. Appl. Cryst., 2016; 50: 776-786] (later it was also applied to mass spectrometry data [A. Mikhalychev et al., Ultramicroscopy, 2020, 215, 113014]).
The idea of the developed approach is schematically shown in Figure 1. We start from a rough estimate of the sample model. The initial information about the investigated sample (zeroth approximation of the lattice constants or superlattice period) is encoded in prior probabilities for the sample model parameters. Based on the measured data, the artificial intelligence agent checks different plausible variants of peak indexing, i.e. tries to find the correspondence between the observed peaks in the measured dataset with the Bragg peaks, layer thickness oscillation fringes, or superlattice fringes, expected according to the sample model. Different choices of the peak association are ranked by Bayesian approach according to their likelihood. For that purpose, the expected inaccuracies of the measurement and peak search are characterized by the likelihood function. For a given peak association, posterior probabilities are calculated for the acceptable sample models, and the probability of the most likely model is used for ranking the current choice of peak indexing. Finally, the peak indexing and the sample model yielding the maximal posterior probability are selected as the optimal solution.
The algorithm, constructed on the basis of the proposed Bayesian approach under the assumption of independent position and intensity errors of individual peaks, was applied to measured and simulated data (Figures 2-4). The performed testing proved applicability and robustness of the algorithm. Moreover, by varying the probability models, one can construct different peak indexing algorithms, suitable for different types of the measured input data. Using artificial intelligence instead of manual peak indexing not only enables faster analysis with much less operator’s efforts, but also provides robustness and reproducibility of the obtained results.
The results have been presented at the 14th Biennial Conference on High-Resolution X-Ray Diffraction and Imaging (XTOP2018, Bari, Italy, 3-7 September 2018): A. Mikhalychev, N. Lappo, M. Zimmermann, A. Benedix, A. Ulyanenkov, Bayesian approach to automatic peak indexing in HRXRD, XTOP2018.
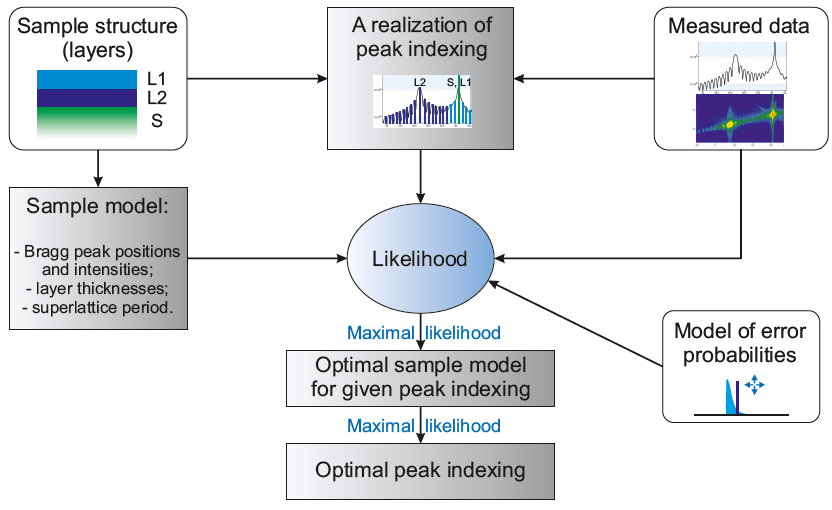
Figure 1. Schematic description of the Bayesian approach to automatic peak indexing.
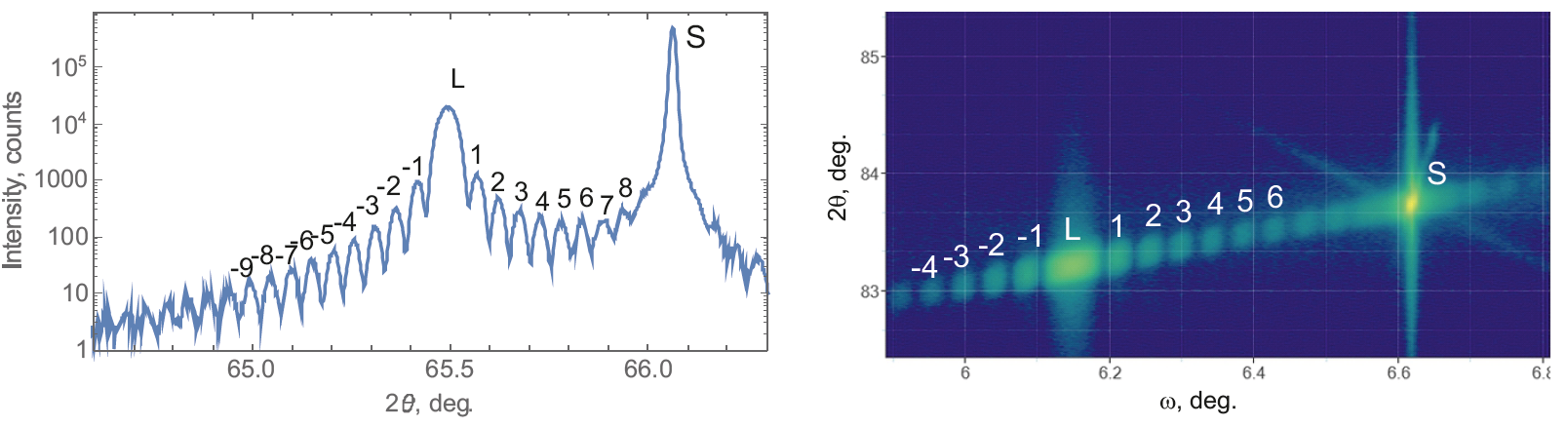
Figure 2. Automatic peak indexing of a measured profile and map for In0.06Ga0.94As layer on GaAs substrate. S – Bragg peak of the substrate; L – Bragg peak of the layer; numbers – layer thickness oscillation fringes.
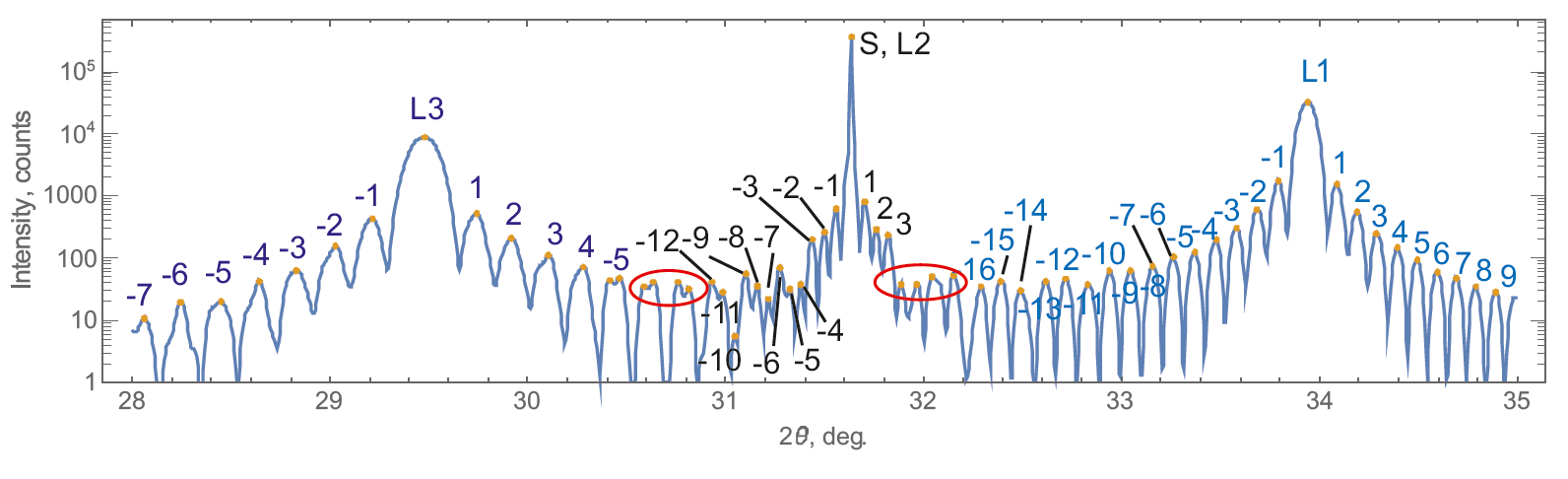
Figure 3. Automatic peak indexing of a simulated profile for In0.5Ga0.5As (L3), GaAs (L2), Al0.5Ga0.5P (L1) multilayer structure on GaAs substrate. S – Bragg peak of the substrate; Li – Bragg peak of the i-th layer; numbers – layer thickness oscillation fringes. Red circles indicate the interference regions, where the model of independent patterns of the layers fails.
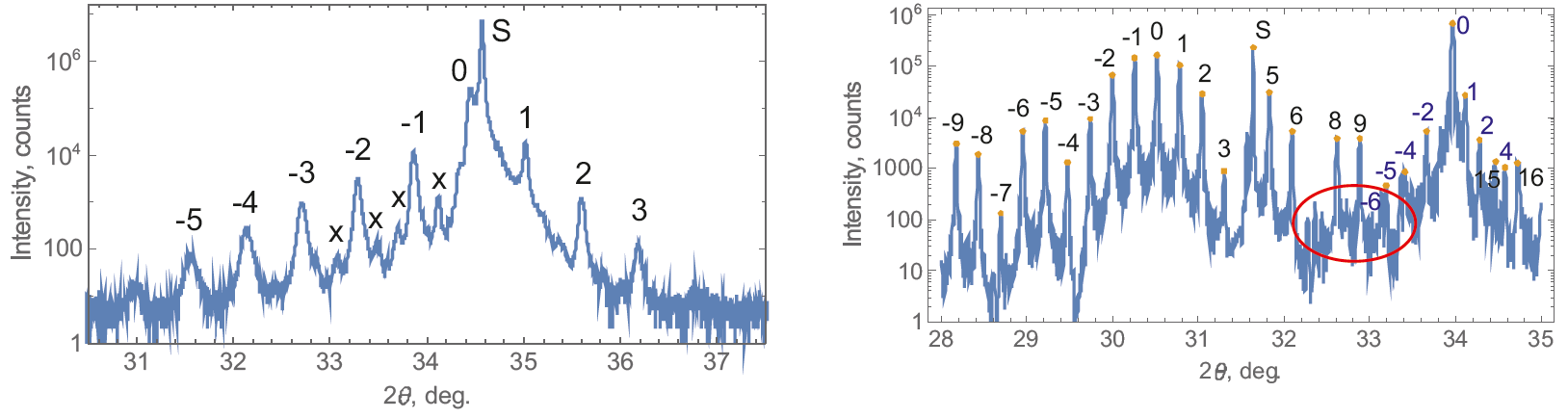
Figure 4. Automatic peak indexing of a measured profile for GaN superlattice (left) and a simulated profile with two superlattices (right). S – Bragg peak of the substrate; numbers – superlattice fringes. Red circle indicates the interference region, where the model of independent patterns of the two superlattices fails.


